Click to learn more about author Kartik Patel.

Multiple Linear Regression is a statistical technique that is designed to explore the relationship between two or more variables (X and Y). It is useful in identifying important factors (X) that will impact a dependent variable (Y) and the nature of the relationship between each of the factors and the dependent variable.

Linear regression is limited to predicting numeric output so the dependent variable has to be numeric in nature. The minimum sample size is 20 cases per independent variable.

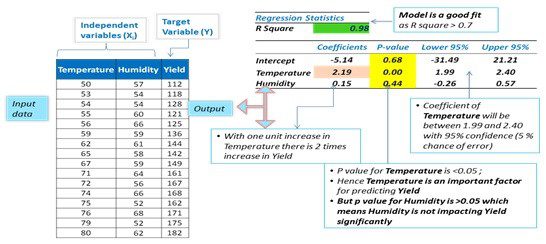
To better understand multiple linear regression, let’s look at one such analysis of independent variables: Temperature and Humidity, and a target variable: Yield.

How Can Multiple Linear Regression Be Helpful for Business Analysis?

If we consider the use cases below, we can see the value of Multiple Linear Regression analysis.

Use Case 1

Business Problem: An ecommerce company wants to measure the impact of product price, product promotions, and holiday seasonality on product sales.

Input Data: Predictor/independent variables include product price data, product promotions data such as discounts, flag representing presence/absence of seasonality. The dependent variable is product sales data.

Business Benefit: A product sales manager can discover which predictors included in the analysis will have significant impact on product sales. For the predictors with the most impact, the team can make important strategic decisions to meet product sales targets. For instance, if promotions and holiday seasons are significant factors, these factors should be given more focus when devising a marketing strategy.

Use Case 2

Business Problem: An agriculture production firm wants to predict the impact of the amount of rainfall, humidity, and temperature on the yield of a particular crop.

Input Data: Predictor/independent variables include the amount of rainfall during monsoon months, the humidity levels/measurements, and the temperature measurements. The dependent variable is crop production.

Business Benefit: An agriculture firm can understand the impact of each of these predictors on the target variable. For instance, if temperature and rainfall have a positive significant impact but humidity levels have a negative significant impact on crop yield, then crop production can be expected during high temperature and rainfall levels in conjunction with low humidity levels.

Multiple linear regression models are useful in helping an enterprise to consider the impact of multiple independent predictors and variables on a dependent variable and can be beneficial for forecasting and predicting results.