Click to learn more about Adam Pease.

Preface

This is the first in a series of articles exploring knowledge representation in Artificial Intelligence from the perspective of a practical implementer and programmer. AI is now a collection of approaches that has seen practical commercial application in search, linguistics, reasoning and analytics in a wide variety of industries. How we represent knowledge in a computer affects how our applications perform, which algorithms we choose, and in fact whether the applications can be successful.

Graphs have long been a popular mechanism in AI for encoding knowledge about the world. In their simplest form there are just nodes and arcs and each can have labels. Often termed ”semantic networks” they offer visually appealing and intuitive way to represent cognitive-level information that is suitable for computer manipulation, and also easy for people to inspect. Google has also reinvigorated this approach with the success of their ”knowledge graph”, leading many to adopt it in their own projects.

Every model has limitations, so in this article and successive ones I attempt to explain what problems may be encountered, so that people can be aware of and avoid pitfalls resulting from application of this technology.

Non-binary relations: between

Let’s look at a very simple problem of network representation. The relationship ”between” is fundamentally among three things – a center object and one object on either side. It’s also a very common thing to say when one is talking about navigating the physical world – travelling from one point to another, designing the layout of a room or building or set of buildings, or even describing events over time.

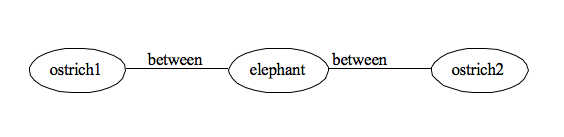
How can this be represented in a semantic network? Given the example shown in Figure 1, we might have a link called ”between” and the graph shown in Figure 2.

Figure 1: An elephant between two ostriches

Figure 2: Network encoding ”between,” version 1

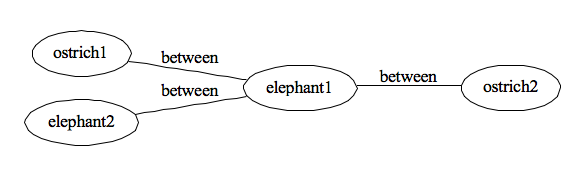
Looking at each pair of nodes, we don’t know which node is in the center. We have to search the network to try to find a pair of ”between” nodes to determine which is the center node. Let’s say however that we add that to a set of rules or procedures that govern the meaning of the network. But what happens when we have a set of objects (Figure 3) and try to represent their relationships with this graph-based approach (Figure 4).

Figure 3: Ostrich1, Elephant2, Elephant1 and Ostrich2 combined

Figure 4: Network encoding ”between,” version 2

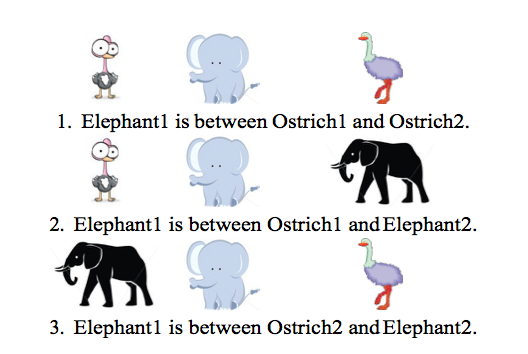
What if we just wanted to say sentences 1 and 3 in Figure 6, which combined would look like Figure 3? There is no way to avoid the additional interpretation of sentence 2 in Figure 6, even though that doesn’t follow from the actual physical arrangement of the animals.

Figure 6: Examples of ”between” that can be reconstructed from the representation in Figure 4. Examples 1 and 3 are true, but not example 2.

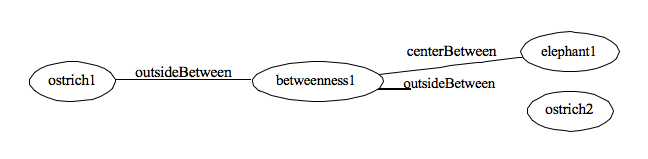
The only approach that allows us to stick with the network formalism is to represent the instance of ”betweenness” and coin two new relations of being at the ”centerBetween” and the ”outsideBetween,” as shown in Figure 5. While this is feasible, it should start to illustrate how one then loses the simplicity and visible perspicuity that is a dominant advantage for network representations.

Figure 5: Network encoding ”between,” version 3

In future articles, I’ll describe some other facts that don’t have a hack in graphs, can’t be represented with simple networks, and require enhancements to the formalism. Stay tuned!